代码随想录算法训练营第四天记录

本文发布于：2022年12月31日

字数：1.8k字

时长：7分钟

在之前刷力扣的过程中，我每刷道题都是先看题解然后再去边写边看，很多内容根本没消化，在进度上欺骗自己，感觉之前刷的都忘了，能力没有什么提升，现在还是一道都不会做。所以这次报了卡哥的算法训练营，希望能够按计划地有效刷题。本次刷题，我用的是 Java 语言解题，有余力的话也可能会加上 C++ 的题解。以下是算法训练营第四天的刷题记录和思考笔记。

一、24 两两交换链表中的节点

题目

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

1 2	输入：head = [1,2,3,4] 输出：[2,1,4,3]

解题思路

用虚拟头结点的方式进行操作，这样会方便很多。

class Solution {
    public ListNode swapPairs(ListNode head) {
        ListNode dummy = new ListNode(-1, head);
        ListNode current = dummy;
        while (current.next != null && current.next.next != null) {
            ListNode temp = head.next.next;    
            current.next = head.next;        
            head.next.next = head;        
            head.next = temp;        
            current = head;					
            head = head.next;				
        }
        return dummy.next;
    }
}

二、19 删除链表的倒数第 N 个节点

题目

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

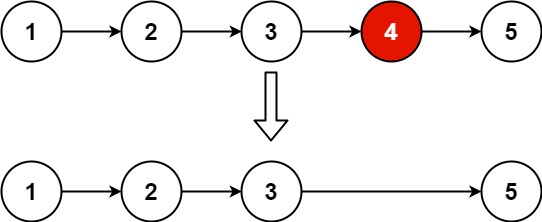
1 2	输入：head = [1,2,3,4,5], n = 2 输出：[1,2,3,5]

解题思路

同样使用虚拟头结点，这样方便处理删除实际头结点的逻辑。定义 fast 指针和 slow 指针，初始值为虚拟头结点，fast 首先走n + 1 步，指向删除节点的下一个节点，这样同时移动的时候 slow 才能指向删除节点的上一个节点（方便做删除操作）。

然后，fast 和 slow 同时移动，直到 fast 指向末尾（Null），此时 slow 指向删除节点的上一个节点。删除 slow 指向的下一个节点（slow->next = slow->next->next;）。

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode dummy = new ListNode(-1, head);
        ListNode fast = dummy;
        ListNode slow = dummy;
        for (int i = 0; i < n; i++) {
            fast = fast.next;
        }
        while (fast.next != null) {    //注意这里是 fast.next 不是 fast
            slow = slow.next;
            fast = fast.next;
        }
        slow.next = slow.next.next;
        return dummy.next;
    }
}

三、面试题 02.07 链表相交

题目

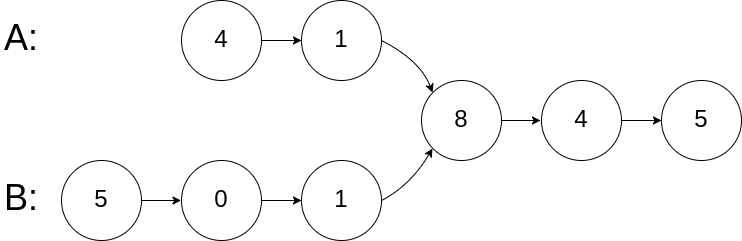
给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。

图示两个链表在节点 c1 开始相交：

题目数据保证整个链式结构中不存在环。注意，函数返回结果后，链表必须保持其原始结构。

输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at '8'
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,0,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

解题思路

简单来说，就是求两个链表交点节点的指针。这里注意，交点不是数值相等，而是指针相等。

使用双指针的方法，可以将空间复杂度降至 O(1)。

只有当链表 headA 和 headB 都不为空时，两个链表才可能相交。因此首先判断链表 headA 和 headB 是否为空，如果其中至少有一个链表为空，则两个链表一定不相交，返回 null。

当链表 headA 和 headB 都不为空时，创建两个指针 pA 和 pB，初始时分别指向两个链表的头节点 headA 和 headB，然后将两个指针依次遍历两个链表的每个节点。

每步操作需要同时更新指针 pA 和 pB。如果指针 pA 不为空，则将指针 pA 移到下一个节点；如果指针 pB 不为空，则将指针 pB 移到下一个节点。如果指针 pA 为空，则将指针 pA 移到链表 headB 的头节点；如果指针 pB 为空，则将指针 pB 移到链表 headA 的头节点。当指针 pA 和 pB 指向同一个节点或者都为空时，返回它们指向的节点或者 null。

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode A = headA, B = headB;
        while (A != B) {
            A = A != null ? A.next : headB;
            B = B != null ? B.next : headA;
        }
        return A;
    }
}

四、142 环形链表 II

题目

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。不允许修改链表。

1
2
3

输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

解题思路

可以使用快慢指针法判断链表是否环，分别定义 fast 和 slow 指针，从头结点出发，fast 指针每次移动两个节点，slow 指针每次移动一个节点，如果 fast 和 slow 指针在途中相遇，说明这个链表有环。这是因为 fast 是走两步，slow 是走一步，其实相对于 slow 来说，fast 是一个节点一个节点的靠近 slow 的，所以 fast 一定可以和 slow 重合。

设链表中环外部分的长度为 a。slow 指针进入环后，又走了 b 的距离与 fast 相遇。此时，fast 指针已经走完了环的 n 圈，因此它走过的总距离为 $a+n(b+c)+b=a+(n+1)b+nc$。

又因为任意时刻，fast 指针走过的距离都为 slow 指针的 2 倍。因此，可以推导出：

$a+(n+1)b+nc=2(a+b)⟹a=c+(n−1)(b+c)$

即从相遇点到入环点的距离加上 $n-1$ 圈的环长，恰好等于从链表头部到入环点的距离。

因此，当发现 slow 与 fast 相遇时，我们再额外使用一个指针 ptr。起始，它指向链表头部。随后，它和 slow 每次向后移动一个位置。最终，它们会在入环点相遇。

public class Solution {
    public ListNode detectCycle(ListNode head) {
        if (head == null) {
            return null;
        }
        ListNode slow = head, fast = head;
        while (fast != null) {
            slow = slow.next;
            if (fast.next != null) {
                fast = fast.next.next;
            } else {
                return null;
            }
            if (fast == slow) {
                ListNode ptr = head;
                while (ptr != slow) {
                    ptr = ptr.next;
                    slow = slow.next;
                }
                return ptr;
            }
        }
        return null;
    }
}

LeetCode

Bezhuang

代码随想录算法训练营第六天记录

在之前刷力扣的过程中，我每刷道题都是先看题解然后再去边写边看，很多内容根本没消化，在进度上欺骗自己，感觉之前刷的都忘了，能力没有什么提升，现在还是一道都不会做。所以这次报了卡哥的算法训练营，希...

代码随想录算法训练营第三天记录